Implementation details

Rayleigh number

The Rayleigh number relates the relative importance of buoyancy forces to diffusive forces, and is an important dimensionless number in convection. Slim (2014) showed that increasing the Rayleigh number increases the number of flow regimes that the convective mixing process goes through.

In the dimensionless model implemented in Numbat, the Rayleigh number appears in the vertical position of the bottom boundary only (Slim, 2014). As a result, it is simple to vary the Rayleigh number in the dimensionless model by simply extending the mesh in the vertical direction.

In the dimensional model, the Rayleigh number may be varied by changing the various physical parameters present, such as permeability, fluid viscosity etc.

Mesh considerations

The process of density-driven convective mixing in porous media begins initially as diffusive mass transfer across the interface between a saturated fluid lying atop an unsaturated fluid. After a sufficient time, the gravitational instability grows until small downwelling fingers of saturated fluid descend into the unsaturated fluid. As time continues, these fingers grow and merge, forming larger fingers. The temporal evolution of this process is shown in Figure 1. The top image shows an initial diffusive profile. As time increases, fingers form, merge and grow in a complex manner.

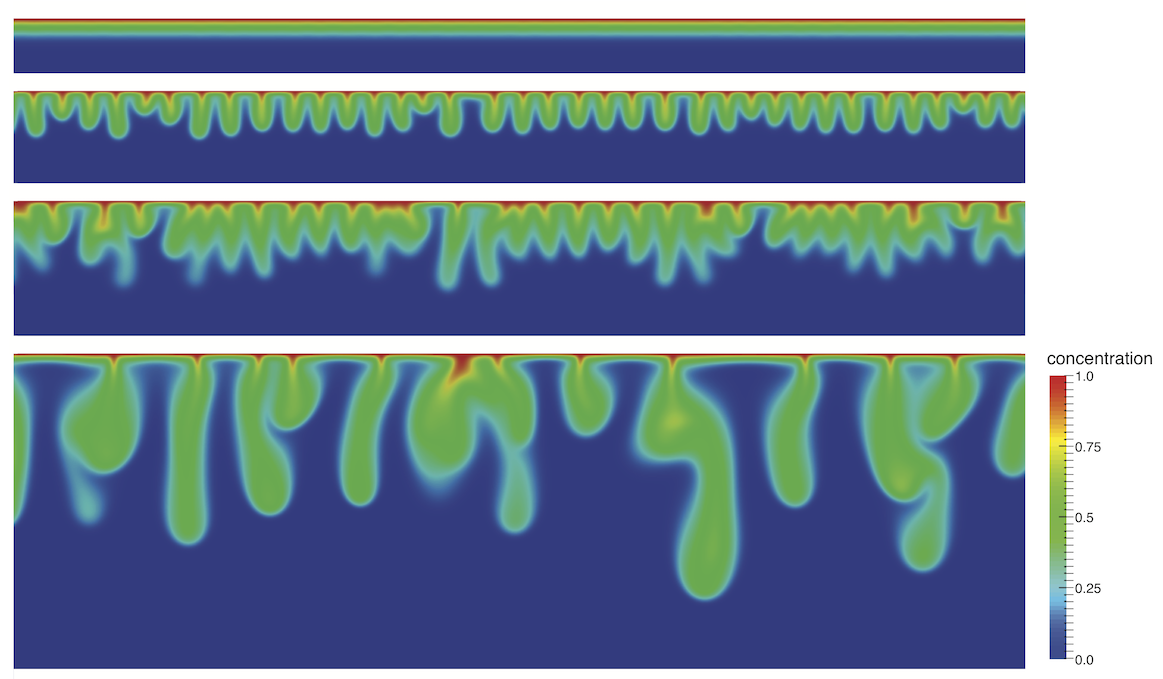
Figure 1: Evolution of convective dissolution (time increasing downwards). Note that the scale is identical for all images.

It is apparent from the temporal evolution above that the mesh requirements differ in different regimes. Early on and near the top of the mesh, the elements must be sufficiently refined to capture the initial formation of small fingers. Later on, and away from the top boundary, larger elements may adequately capture the large downwelling fingers, and as such, the mesh may be coarser in this region.

There are two ways that the user may deal with these disparate mesh requirements: use a mesh that is more refined in the vicinity of the top boundary; or use adaptive mesh refinement. Both of these are possible in Numbat.

Numbat provides a type of GeneratedMesh where the elements are biased towards the top boundary, NumbatBiasedMesh, so that it is more refined in the vicinity of the constant concentration boundary. This is particularly useful in two dimensions.

For three-dimensional models, an external meshing code may be used to generate an unstructured mesh. MOOSE can read a number of mesh formats natively, see the MOOSE documentation for details. One open-source option for generating unstructured meshes that MOOSE can read is Gmsh. An example of a fully unstructured 3D mesh that is refined near the top boundary and coarse near the bottom boundary is shown in Figure 2.

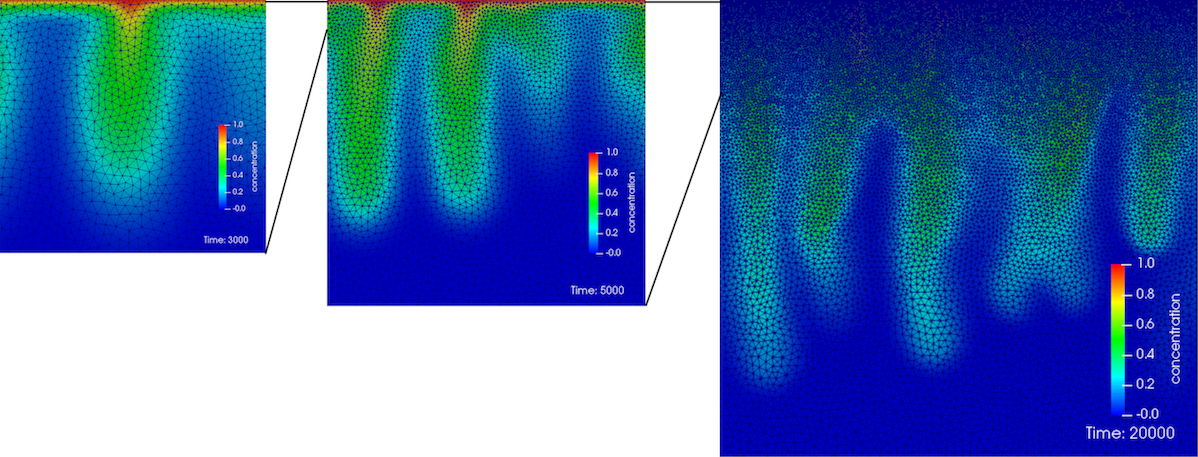
Figure 2: Example of unstructured mesh used in Numbat that was generated by Gmsh. Leftmost image shows small section near the top with the concentration profile at an early time; middle image shows top quarter of full mesh and concentration profile at an intermediate time; rightmost image shows full mesh and concentration profile at late time.

Seeding the perturbation

Numerical simulations of solutal convection rely on seeding the gravitational instability to initiate the convective mixing process. Numerical roundoff will eventually initiate convective mixing, but can significantly overestimate the critical time for the onset of convection.

Instead, it is usual to seed the instability using a prescribed random perturbation in the model. Several types of perturbation have been considered in the literature, see Emami-Meybodi et al. (2015) for a detailed review.

In Numbat, an initial perturbation to seed the instability can be applied in several ways:

• In the dimensional formulation, a random noise sampled from a uniform distribution can be applied to the porosity;

• In the dimensionless streamfunction formulation, an initial perturbation to the diffusive concentration profile can be applied;

• A random fluctuation to the concentration boundary condition can be applied.

The strength of the initial perturbation has been shown to affect the initial onset time for convection, see Emami-Meybodi et al. (2015) for details. This should be taken into consideration when modelling convective mixing in porous media.

References

1. Hamid Emami-Meybodi, Hassan Hassanzadeh, Christopher P. Green, and Jonathan Ennis-King. Convective dissolution of CO$_2$ in saline aquifers: Progress in modeling and experiments. International Journal of Greenhouse Gas Control, 40:238–266, 2015.[BibTeX]

   @article{emami-meybodi2015,
       author = "Emami-Meybodi, Hamid and Hassanzadeh, Hassan and Green, Christopher P. and Ennis-King, Jonathan",
       title = "{Convective dissolution of CO$\_2$ in saline aquifers: Progress in modeling and experiments}",
       journal = "International Journal of Greenhouse Gas Control",
       volume = "40",
       pages = "238--266",
       year = "2015"
   }
   

2. A.C. Slim. Solutal-convection regimes in a two-dimensional porous medium. J. Fluid Mech., 741:461–491, 2014.[BibTeX]

   @article{slim2014,
       author = "Slim, A.C.",
       title = "Solutal-convection regimes in a two-dimensional porous medium",
       journal = "J. Fluid Mech.",
       volume = "741",
       pages = "461--491",
       year = "2014"
   }