ConservativeAdvection

Description

The ConservativeAdvection kernel implements an advection term given for the domain () defined as

(1) where is the advecting velocity and the second term on the left hand side represents the strong forms of other kernels. ConservativeAdvection does not assume that the velocity is divergence free and instead applies to the test function in the weak variational form after integrating by parts, which results in the following (without numerical stabilization)

(2) where are the test functions and is the finite element solution of the weak formulation. The first term is the volumetric term and the second term is a surface term describing the advective flux out of the volume. ConservativeAdvection corresponds to the former volumetric term, while the surface term is implemented as a BC in MOOSE (see discussion below regarding OutflowBC and InflowBC).

Without numerical stabilization the corresponding Jacobian is given by

(3)

Full upwinding

Advective flow is notoriously prone to physically-incorrect overshoots and undershoots, so in many simulations some numerical stabilization is used to reduce or eliminate this spurious behaviour. Full-upwinding Dalen (1979) and Adhikary and Wilkins (2011) is an example of numerical stabilization and this essentially adds numerical diffusion to completely eliminate overshoots and undershoots. Full-upwinding is available in ConservativeAdvection by setting the upwinding_type appropriately.

In DE systems describing more than just advection (e.g., in diffusion-advection problems) full upwinding may be used on the advection alone. In practise, it is reasonably common that these more complicated cases benefit from numerical stabilization on their other terms too, in which case full upwinding could also be used, but this is not mandatory and is not implemented in the ConservativeAdvection Kernel.

For each element in the mesh, full upwinding is implemented in the following way. For each , the quantity (4) is evaluated. If is positive then mass (or heat, or whatever represents) is flowing out of node , and this is called an "upwind" node. If , the residual for node is set to (5) Here is the value of at the node . Define the total mass flowing from the upwind nodes: (6) Similarly, define (7) Mass is conserved if the residual for the downwind nodes is defined to be (8)

Full upwinding adds more numerical diffusion than most other numerical stabilization techniques such as SUPG and TVD. Another problem is that steady-state can be hard to achieve in nonlinear problems where the velocity is not fixed and changes every nonlinear iteration (this does not occur for ConservativeAdvection). On the other hand, full upwinding is computationally cheap.

Example Syntax

ConservativeAdvection can be used in a variety of problems, including advection-diffusion-reaction. The syntax for ConservativeAdvection is demonstrated in this Kernels block from a pure advection test case:

[Kernels]
  [./udot]
    type = TimeDerivative
    variable = u
  [../]
  [./advection]
    type = ConservativeAdvection
    variable = u
    velocity = '1 0 0'
  [../]
[]

The velocity is supplied as a three component vector with order , , and .

Boundary conditions for pure advection

To form the correct equations, the boundary term needs to be included in the BCs block of a MOOSE input file ( is the outward normal to the boundary). An OutflowBC may be used, for instance

[BCs]
  [./allow_mass_out]
    type = OutflowBC
    boundary = right
    variable = u
    velocity = '1 0 0'
  [../]
[]

Physically this subtracts "fluid mass" (or whatever represents) from the boundary.

For adding the OutflowBC allows "fluid" to flow freely through the boundary. The advective velocity is "blowing fluid" into this boundary, and the OutflowBC is removing it at the correct rate, because the flux through any area is .

On the other hand, including an OutflowBC for isn't usually desirable. Adding the OutflowBC in this case fixes at the boundary to its initial condition. This is because the ConservativeAdvection Kernel is taking fluid from the boundary to the interior of the model, but at the same time the OutflowBC is removing : note that , so the OutflowBC is actually adding fluid at the same rate the ConservativeAdvection Kernel is removing it. The physical interpretation is that something external to the model is adding fluid at exactly the rate specified by the initial conditions at that boundary.

Instead, for users typically want to specify a particular value for an injected flux. This is achieved by using an InflowBC. This adds , where (kg.m.s) is the injection rate. For instance

[BCs]
  [./u_injection_left]
    type = InflowBC
    boundary = left
    variable = u
    velocity = '1 0 0'
    inlet_conc = 1
  [../]
[]

To make impermeable boundaries, either for or , simply use no BC at that boundary. Then for there is no BC to remove fluid from that boundary so the fluid "piles up" there. For the omission of a BC can be thought of setting in an InflowBC.

Comparison of no upwinding and full upwinding

The tests

# ConservativeAdvection with upwinding_type = None
# Apply a velocity = (1, 0, 0) and see a pulse advect to the right
# Note there are overshoots and undershoots
[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = 10
[]

[Variables]
  [./u]
  [../]
[]

[BCs]
  [./u_injection_left]
    type = InflowBC
    boundary = left
    variable = u
    velocity = '1 0 0'
    inlet_conc = 1
  [../]
[]

[Kernels]
  [./udot]
    type = TimeDerivative
    variable = u
  [../]
  [./advection]
    type = ConservativeAdvection
    variable = u
    velocity = '1 0 0'
  [../]
[]

[Executioner]
  type = Transient
  solve_type = LINEAR
  dt = 0.1
  end_time = 1
  l_tol = 1E-14
[]

[Outputs]
  exodus = true
[]

and

# ConservativeAdvection with upwinding_type = full
# Apply a velocity = (1, 0, 0) and see a pulse advect to the right
# Note that the pulse diffuses more than with no upwinding,
# but there are no overshoots and undershoots and that the
# center of the pulse at u=0.5 advects with the correct velocity
[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = 10
[]

[Variables]
  [./u]
  [../]
[]

[BCs]
  [./u_injection_left]
    type = InflowBC
    boundary = left
    variable = u
    velocity = '1 0 0'
    inlet_conc = 1
  [../]
[]

[Kernels]
  [./udot]
    type = MassLumpedTimeDerivative
    variable = u
  [../]
  [./advection]
    type = ConservativeAdvection
    variable = u
    velocity = '1 0 0'
    upwinding_type = full
  [../]
[]

[Executioner]
  type = Transient
  solve_type = LINEAR
  dt = 0.1
  end_time = 1
  l_tol = 1E-14
[]

[Outputs]
  exodus = true
[]

describe the same physical situation: advection from left to right along a line. A source at the left boundary introduces into the domain at a fixed rate (using an InflowBC). The right boundary is impermeable (no BC), so when arrives there it starts building up at the boundary. It is clear from the figures below that no upwinding leads to unphysical overshoots and undershoots, while full upwinding results in none of that oscillatory behaviour but instead produces more numerical diffusion.

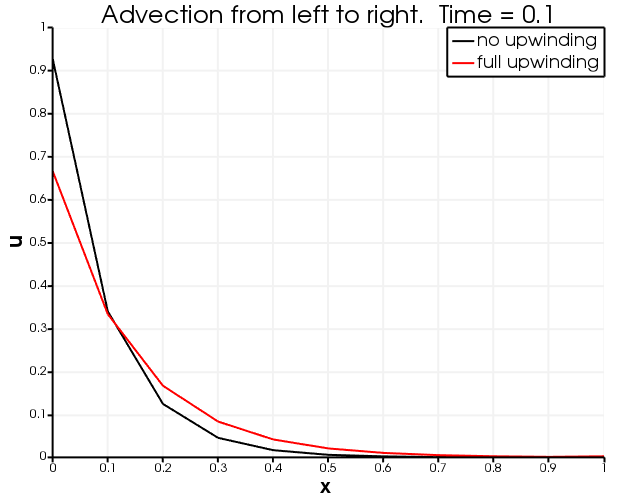
after 0.1 seconds of advection

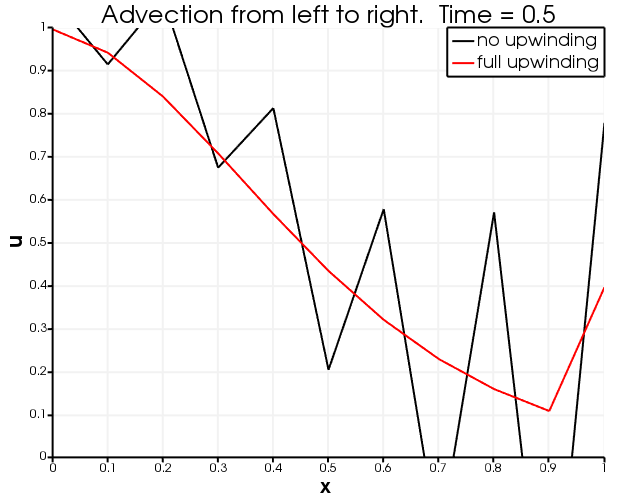
after 0.5 seconds of advection

Input Parameters

References

1. D. Adhikary and A. Wilkins. Analysis of finite element discretisation schemes for multi-phase Darcy flow. Defect and Diffusion Forum, 318:33–40, 2011. doi:10.4028/www.scientific.net/DDF.318.33.[BibTeX]

   @article{adhikary2011,
       author = "Adhikary, D. and Wilkins, A.",
       abstract = "We demonstrate that care must be taken in a finite element discretisation of multi-phase compressible Darcy flow, otherwise constraints of non-negativity of fluid mass can become violated. Generalising a technique pioneered by Dalen, a lumped, finite-difference-inspired approximation with upstream weighting is described. This is numerically cheap, physically elegant, and the fluid mass at all nodes remains non-negative.",
       doi = "10.4028/www.scientific.net/DDF.318.33",
       journal = "Defect and Diffusion Forum",
       pages = "33--40",
       title = "{Analysis of finite element discretisation schemes for multi-phase Darcy flow}",
       volume = "318",
       year = "2011"
   }
   

2. ~V. Dalen. Simplified Finite-Element Models for Reservoir Flow Problems. Society of Petroleum Engineers Journal, 19:333–342, 1979. doi:10.2118/7196-PA.[BibTeX]

   @article{dalen1979,
       author = "Dalen, \textasciitilde V.",
       abstract = "This paper summarizes some research that was conducted to construct finite-element models for reservoir flow problems. The models are based on Galerkin's method, but the method is applied in an unorthodox manner to simplify calculation of coefficients and to improve stability. Specifically, techniques of compatibility relaxation, capacity lumping, and upstream mobility weighting are used, and schemes are obtained that seem to combine the simplicity and high stability of conventional finite-difference models with the generality and modeling flexibility of finite-element methods. The development of a model for single-phase gas flow and a two-phase oil/water model is described. Numerical examples are included to illustrate the usefulness of finite elements. In particular, the triangular element with linear interpolation is shown to be an attractive alternative to the standard five-point, finite-difference approximation for two-dimensional analysis.",
       doi = "10.2118/7196-PA",
       journal = "Society of Petroleum Engineers Journal",
       pages = "333-342",
       title = "{Simplified Finite-Element Models for Reservoir Flow Problems}",
       volume = "19",
       year = "1979"
   }